Thomson scattering near sunspots: Difference between revisions
imported>Hhudson |
imported>Hhudson (suthor's fixes) |
||
| Line 6: | Line 6: | ||
|second_author = et al. | |second_author = et al. | ||
|publish_date = 25 October 2021 | |publish_date = 25 October 2021 | ||
|next_nugget = | |next_nugget = ALMA-IRIS-HInode Microflares | ||
|previous_nugget = {{#ask: [[Category:Nugget]] [[RHESSI Nugget Index::418]]}} | |previous_nugget = {{#ask: [[Category:Nugget]] [[RHESSI Nugget Index::418]]}} | ||
}} | }} | ||
| Line 26: | Line 26: | ||
In fact the solar radiation incident on the low corona can be highly non-radial | In fact the solar radiation incident on the low corona can be highly non-radial | ||
in the vicinity of a sunspot group, most importantly simply because the | in the vicinity of a sunspot group, most importantly simply because the | ||
sunspot will normally NOT lie directly on the radial line. | sunspot will normally NOT lie directly on the radial line (the line connecting Sun center with the scatterer). | ||
The continuum brightness of a sunspot is much less than that of the quiet | The continuum brightness of a sunspot is much less than that of the quiet | ||
photosphere, and of course its emission spectrum also differs radically. | photosphere, and of course its emission spectrum also differs radically. | ||
| Line 81: | Line 81: | ||
sunspot at a given displacement in latitude and longitude from the scatterer's | sunspot at a given displacement in latitude and longitude from the scatterer's | ||
position. | position. | ||
The quantity G shown in the maps is the emissivity normalized by the Thomson cross-section, the photospheric intensity, and the electron | |||
density at the scattering point, and the subscript denotes the Stokes component. | |||
These maps show strong dependence both on spot location (with respect to the | These maps show strong dependence both on spot location (with respect to the | ||
vantage point) and on limb darkening. | vantage point) and on limb darkening. | ||
Ergo, actual observations would help to characterize these physical parameters. | Ergo, actual observations would help to characterize these physical parameters. | ||
Note that limb darkening at the | Note that limb darkening at the extreme limb, while very important | ||
photometrically, is very hard to observe directly. | photometrically, is very hard to observe directly. | ||
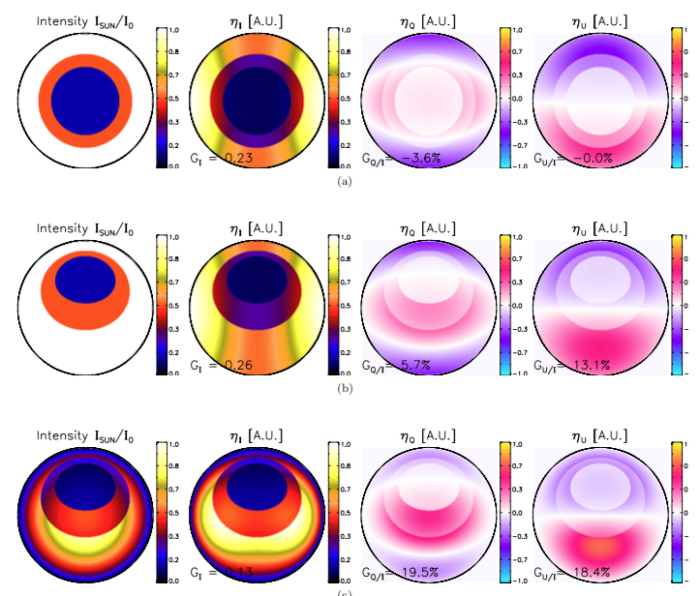
[[File:419f1.png| | [[File:419f1.png|700px|thumb|center|<b>Figure 1:</b> | ||
<i> | <i> | ||
Emissivity maps in helioprojective coordinates. | Emissivity maps in helioprojective coordinates. | ||
| Line 93: | Line 95: | ||
The observer (at Earth) is to the far left, from the reader's (and the | The observer (at Earth) is to the far left, from the reader's (and the | ||
scatterer's) perspective. | scatterer's) perspective. | ||
Left, the map showing a spot with umbral diameter 30,000 km and penumbral | Left, the map showing a model spot with umbral diameter 30,000 km and penumbral | ||
diameter 51,000 km; right, the Stokes I, Q and U emissivities. | diameter 51,000 km; right, the Stokes I, Q and U emissivities. | ||
From top to bottom: symmetry, displacement by two degrees and no limb | From top to bottom: symmetry, displacement by two degrees and no limb | ||
| Line 99: | Line 101: | ||
</i> | </i> | ||
]] | ]] | ||
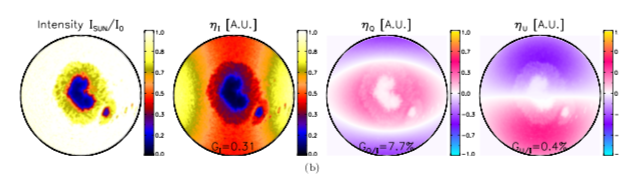
The detailed calculation for an actual sunspot configuration appears in Figure 2. | |||
This shows the same view as Figure 1, for the case vertically above the spot group at a height of 28,000 km | |||
and with standard photospheric limb darkening. | |||
[[File:419f2.png|800px|thumb|center|<b>Figure 1:</b> | |||
<i> | |||
The same calculation for an actual sunspot pattern, as viewed at 28,000 km and with standard limb darkening. | |||
</i> | |||
]] | |||
Generally Q/I will be smaller with spots than in the spotless case. | |||
U/I will become non-zero if a sunspot is present (except if scattering element is smack in the middle | |||
of an axisymmetric sunspot). | |||
== Conclusions == | == Conclusions == | ||
Latest revision as of 14:36, 2 November 2021
| Nugget | |
|---|---|
| Number: | 419 |
| 1st Author: | Pascal SAINT-HILAIRE |
| 2nd Author: | et al. |
| Published: | 25 October 2021 |
| Next Nugget: | ALMA-IRIS-HInode Microflares |
| Previous Nugget: | A Non-PFSS Global Coronal Model |
Introduction
We detect the solar corona in many ways, but among the most fundamental we find the "K-corona" component via Thomson scattering of photospheric light by free electrons. Minnaert originally described the application of this theory to the solar corona in Ref. [1], and we note that its nature (hot or cold? Electrons free or bound?) was really not understood at that time. His theory described the intensity and (linear) polarization of the scattering process, but not in full generality.
These calculations assumed radial symmetry. In fact the solar radiation incident on the low corona can be highly non-radial in the vicinity of a sunspot group, most importantly simply because the sunspot will normally NOT lie directly on the radial line (the line connecting Sun center with the scatterer). The continuum brightness of a sunspot is much less than that of the quiet photosphere, and of course its emission spectrum also differs radically. This Nugget describes the extension of Minnaert's theory to accommodate this effect.
We note that normally sunspots do not matter much, since coronagraphic fields of view typically have inner radial limits well above the photosphere. Recently, however, it has become possible to observe "white light prominencs" - flare loops seen in the visible continuum - routinely via the HMI imagery (Ref. [2]). These data characterize the full Stokes parameter set, including the linear polarization that is the key to the electron-scattering brightness. In this Nugget we describe, we think for the first time, the effects of sunpots on the polarization observed in white-light prominences by HMI (Ref. [3]).
Sunspot Effects
When we observe an active region at (or near) the limb, its magnetic structure projects against the dark sky and becomes visible at various wavelengths. Normally the visible continuum is not one of these ways, since these quiet-Sun loops have relatively low densities. With narrow-band observations in the EUV particularly, for example via EUV imagery from the SDO/AIA observations, we can see the direct emission of these loops. In flares the story is different, since we may see "white light prominences" as a part of the mass redistribution ("chromospheric evaporation") into the corona. These flare loops are brightest in the low corona, and if sunspots are nearby the photospheric irradiation of the scattering electrons will be anisotropic. This would be true as well for scattering opacity in certain bound-bound (line) emissions. Roughly speaking, the vertical scale upon which the anisotropy would matter would be comparable to the horizontal scale, in the photosphere, for the inhomogeneous brightness distribution. Thus a 35,000 km sunspot (large) would significantly affect scattered light formed below about 0.1 solar radii (70,000 km).
Ref. [4] describes calculations of model sunspot geometries, and also describes the full calculation based upon an arbitrary photospheric brightness distribution. Of course, we cannot observe this from the Earth perspective; the model calculations of realistic sunspot patterns in Ref. [4] therefore have to assume negligible evolution over a few days. This restriction would be removed if we had stereo view, which may be forthcoming from Solar Orbiter in the foreseeable future.
In the meanwhile, Figure 1 shows model calculations for an ideal round sunspot at a given displacement in latitude and longitude from the scatterer's position. The quantity G shown in the maps is the emissivity normalized by the Thomson cross-section, the photospheric intensity, and the electron density at the scattering point, and the subscript denotes the Stokes component. These maps show strong dependence both on spot location (with respect to the vantage point) and on limb darkening. Ergo, actual observations would help to characterize these physical parameters. Note that limb darkening at the extreme limb, while very important photometrically, is very hard to observe directly.
The detailed calculation for an actual sunspot configuration appears in Figure 2. This shows the same view as Figure 1, for the case vertically above the spot group at a height of 28,000 km and with standard photospheric limb darkening.
Generally Q/I will be smaller with spots than in the spotless case. U/I will become non-zero if a sunspot is present (except if scattering element is smack in the middle of an axisymmetric sunspot).
Conclusions
The calculations of Ref. [4], though they describe the full geometry of the non-radial radiation field, only represent a beginning here. We expect that DKIST and other ground-based observing facilities will need a full spectral description of the non-radial effects in order to deal well with scattering opacity at the limb. These may include major contributions from plage/faculae as well as spots, but there is a snag: limb observations by ground-based telescopes require a complementary stereoscopic vantage point to map out an active region's spots and faculae properly. We hope that this information may come, in some cases, from the recently launched Solar Orbiter.
Authorship
Pascal SAINT-HILAIRE, Juan Carlos MARTÍNEZ OLIVEROS, and Hugh HUDSON
References
[1] "On the continuous spectrum of the corona and its polarisation"
[2] "Chromospheric and Coronal Observations of Solar Flares with the Helioseismic and Magnetic Imager"]
[4] "Thomson scattering in the lower corona in the presence of sunspots"