Photospheric Temperature Gradient
| Nugget | |
|---|---|
| Number: | 186 |
| 1st Author: | Martin Fivian |
| 2nd Author: | Hugh Hudson |
| Published: | 22 October 2012 |
| Next Nugget: | TBD |
| Previous Nugget: | Energy Partition |
Introduction
RHESSI's solar aspect sensors (SAS) have begun to produce scientific results in their own right; these little (4 cm) telescopes have a particular niche in solar astronomy, since they are probably the only rapidly-rotating solar telescopes in space. They observe the Sun at visual wavelengths and therefore measure the brightness (or temperature) of the solar photosphere. RHESSI rotates with a dizzying 4 sec period, and this is a great advantage for precision measurements because it reduces the systematic errors that have plagued, for example, oblateness measurements in the past.
Earlier Nuggets (on the Willson Effect, Optical Images, and Oblateness) have reported on the nature of these data and their first important result published, namely the most accurate determination of the oblateness of the Sun.
Rotation makes a star oblate, and it also makes it appear darker at its equator; this is the result of diminished heat flux, and for non-convective stars the temperature should vary directly with the surface gravity. Hence the poles would be a little hotter and brighter. Even more important and interesting, the inner workings of the Sun that produce solar magnetism (the dynamo) should also produce signatures, perhaps weak, in the temperature distribution of the photosphere. Many searches (see ref. [1]) have sought such signatures.
Observations
The results reported here, for which this Nugget gives a pre-publication glimpse, come from the same four-month interval in 2004 for which we reported our RHESSI results on oblateness (ref. [2]). Both the oblateness result and the temperature result depend upon the very precise fit to the mean profile of the solar limb, as we illustrate in Figure 1.
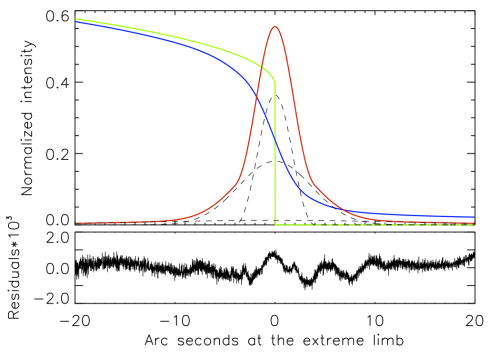
The precise fit to get the exact mean location of the limb leads to the precise photometry needed to detect the latitude dependence of effective temperature. This is because of the limb darkening, by which errors in pixel position can translate into errors in brightness. The RHESSI data do not show a pole-to-equator variation in temperature and only place an upper limit of 0.1 K on the possible total difference (pole minus equator). This result comes from fitting an annular region just inside the limb (at μ = cos(θ) = 0.12) in the manner shown in Figure 2.
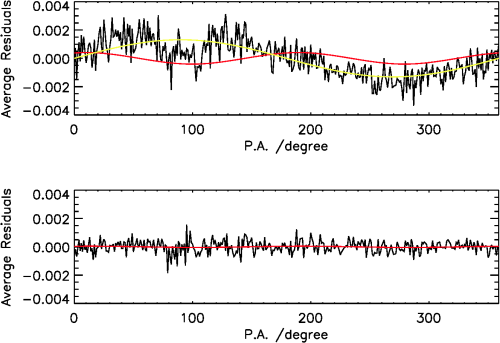
The analysis shown in Figure 2 required a masking against a proxy for magnetic elements. The EIT 284 A images from the SOHO spacecraft work well for this purpose, as shown in the Figure. The masking is necessary in order to restrict the fits to the underlying photosphere itself; magnetic features tend to produce emission excesses (faculae) whose distribution can distort the measurement. Only with a proxy can the faintest of these features be eliminated.
Conclusion
A simple telescope in space, rapidly rotating around its line of sight to the Sun, has provided very tight limits on the possible latitudinal variation of solar effective temperature. Since this initial look used only a few percent of the available data, and since analysis procedures continually improve, this limit will get better and/or RHESSI will actually begin to see real effects. This mapping of mean temperature structures on the surface of the Sun, we hope, will complement the results obtained from helioseismology, and teach us basically new things about the nature of convection and the solar cycle.
References
[1] Latitudinal Variation of Solar Photospheric Intensity
[2] A Large Excess in Apparent Solar Oblateness Due to Surface Magnetism