Advection and super-diffusive expansion as the model of flare accelerated electron transport in type III solar radio bursts
| Nugget | |
|---|---|
| Number: | 481 |
| 1st Author: | Eduard KONTAR |
| 2nd Author: | Francesco AZZOLLINI, Olena LYUBCHYK |
| Published: | |
| Next Nugget: | Flare ribbons at highest resolution |
| Previous Nugget: | Advection and super-diffusive expansion as the model of flare accelerated electron transport in type III solar radio bursts |
Introduction
The signatures of fast (accelerated) electrons associated with solar flare appear over a wide range of frequencies, from low radio frequencies in interplanetary space to the γ-ray range at the Sun. While hard X-ray observations provide the most direct signatures of electron acceleration and propagation in the solar atmosphere, radio observations are uniquely able to trace the electrons in interplanetary space. However, quantitatively describing the electron transport responsible for type III bursts, for example, remains a challenge. These electrons occur in a directed beam flowing outward in the corona and solar wind. Such a beam is unstable and should not exist for long; the characteristic time of a kinetic beam-plasma instability ("quasilinear relaxation") is normally short. This will quickly decelerate such a beam, and yet we observe the type III bursts to persist. This is a long-standing theoretical problem, often referred to as Sturrock's dilemma. Here we describe an analytical solution to this dilemma (Ref. [1]).
Quasilinear theory
Quasilinear theory describes the propagation of electrons along magnetic field lines in a weakly magnetized plasma and their resonant interaction with Langmuir waves. The coupled quasilinear equations provide a kinetic description of electrons and Langmuir waves in type III solar radio bursts. As electrons follow magnetic field lines, the reduced field-aligned electron distribution function and the spectral energy density of the Langmuir waves evolve following nonlinearly coupled kinetic equations. These kinetic equations do not have an analytical solution.
The characteristic time of beam-plasma interaction is normally small, allowing for a hydrodynamic description for beam electrons and Langmuir waves. We expand the electron distribution function in the kinetic equations via a small parameter, similar to the Chapman-Enskog theory of a neutral gas dominated by collisions. The zeroth-order solution is a plateau in velocity space, with the generation of an enhanced level of Langmuir waves is generated. However, the relaxation process is not uniform across space due to the finite size of the electron beam, requiring consideration of spatial variations during the quasilinear time scale. To address the inhomogeneity of quasilinear time, we retain the first-order term in the expansion of the electron distribution function. Integrating the resulting equation over velocity provides a modified equation for particle conservation, incorporating both the advection and the nonlinear diffusion of the electrons. The spatial diffusion coefficient is inversely proportional to the beam density and is smaller for smaller quasilinear time. The diffusion coefficient with a 1/n(x,t) nonlinear dependence on the density is known as "fast diffusion", where diffusion is faster in regions with low particle density.
Results
Intriguingly, an asymptotic solution to the advection-nonlinear-diffusion equation shows that the electron beam propagates at a constant speed with a spatial width that grows over time (Figure 1). This solution describes an expanding electron beam moving with a speed proportional to the initial beam velocity and the minimum velocity of the plateau. The electron beam size grows linearly with time, and the peak density decreases with distance. The spatial expansion of the electron beam leads to a decrease in peak density and the spectral energy density of Langmuir waves, consistent with observations of type III solar radio bursts.
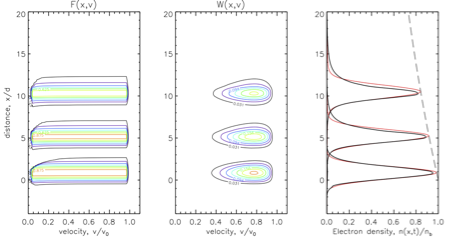
Conclusion
This Nugget describe a quantitative analytical model for electron transport in type III solar radio bursts (Ref. [1]). This model successfully accounts for the finite size of the electron beam and nonlinear diffusion allows to investigate large-scale structural variations of a type-III-burst electron beam. Moreover, the model provides a better fit to numerical simulations (Figure 1) and some observations, showing that the spatial expansion of the electron beam leads to a decrease in peak density and the spectral energy density of Langmuir waves.