How much of the energy in flare-accelerated electrons reaches the chromosphere?

Nugget
Number:	477
1st Author:	M. ALAOUI
2nd Author:	G. HOLMAN
Published:
Next Nugget:	AIA point-spread function and DEM
Previous Nugget:	Spatially resolved plasma composition evolution in a solar flare

Introduction

Weakly relativistic electrons play an important role in solar flares as a mechanism for energy transport. We often treat these electrons as in a thick-target laboratory X-ray source, in which the fast electrons come to a complete stop as they radiate bremsstrahlung photons.

In both the standard (cold) collisional thick target model (CTTM) and the warm-CTTM, Coulomb collisions between the flare-accelerated energetic electron beam and ambient plasma electrons are the primary energy loss mechanism from the injection site down to the chromosphere. However, since these energetic electrons must typically have very large fluxes (on the order of 10³⁴-10³⁶ electrons/s) and propagate from their acceleration site at the looptop to the lower solar atmosphere, they must be accompanied by an oppositely directed return current which is generated as a result of the large charge displacement in the solar corona. The impact of the return current on the beams energy losses has been studied extensively assuming that Ohm's law governs the dynamics of the interaction. Our work (Ref. [1],[2]) examines the conditions under which this is a good assumption and conditions where collisionless effects, especially the acceleration of runaway electrons out of the ambient RC plasma, need to be taken into account.

Energy deposition in the corona vs. the chromosphere

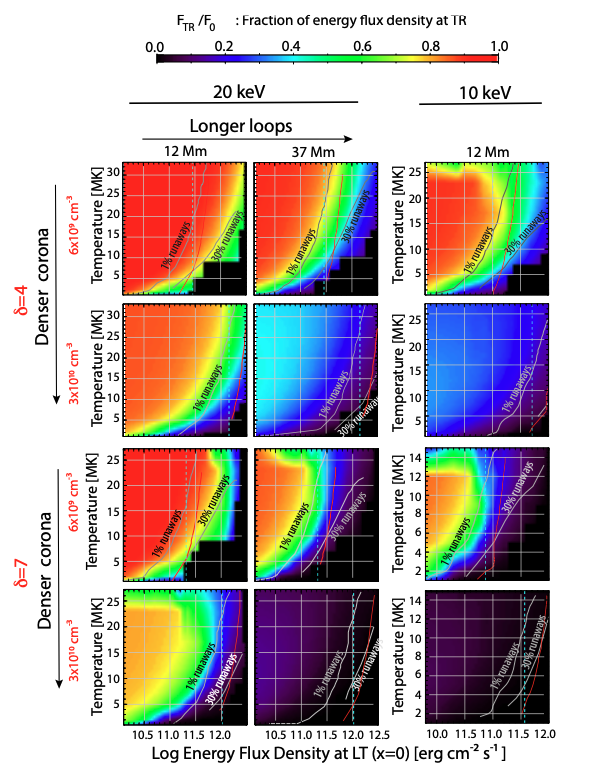
Our earlier work (Ref. [1]) calculates the steady-state field-aligned energy losses in a 1D model, considering Coulomb collisions and return-current deceleration. We include runaway electrons accelerated out of the ambient plasma, in a "warm-target" approximation (see [https://research.ssl.berkeley.edu/~tohban/wiki/index.php/How_to_better_determine_the_power_in_non-thermal_electrons_from_observed_X-ray_spectra Nugget No. 264], for example). This warm-target capability is especially important for lower (and higher) values of the low-energy cutoff (and injected electron power-law spectral index). The calculations not only show the energy deposition in the corona but also the total potential drop in the corona, which can be observed as a flattening in hard X-ray spectra at lower photon energies. We also discuss regions where the return-current losses can be neglected altogether, and alternatively where RC losses are significant and where runaway electrons also need to be included.

Additionally, in Ref. [2], we find

• Implications for initial conditions in atmospheric response calculations: Notice that at lower coronal temperatures and/or densities, collisionless effects are increasingly significant with the injected flux density.

• The conclusion that injected electron flux densities are inconsistent with negligible return current losses at the HXR peak times for two X-class RHESSI flares: SOL2002-Jul-23T00:20 and SOL2006-Dec-06T18:30.

Figure 1 summarizes this work.

Figure 1: Ratio of the nonthermal energy flux density at the transition region to the injected energy flux density at the looptop. Each panel shows calculations using the same low-energy cutoff, spectral index, loop length and coronal density as coronal temperature vs. injected electron energy flux. The various curves represent the conditions for which: (1) the fraction of the return current carried by runaway electrons at the looptop is 1% and 30% (solid gray curves), (2) the maximum return-current electric field magnitude normalized to the Dreicer field is equal to 0.15 (solid red); above this value even our quasi-collisional model is insufficient to account for the dynamics. The vertical dashed lines show the conditions for the energetic electron density to be 10% of the ambient return-current density.

What is the dominant collisionless effect?

Collisionless effects include acceleration of runaway electrons which are included in the model and current-driven instabilities, which are not included so far. However, we show the conditions where these do need to be taken into account. The return-current drift speed varies along the legs of the loop, but comparing its maximum value to the local electron thermal speed is sufficient to test whether the flux density threshold for generating a current-driven instability is met. Figure 2 shows that accelerating runaway electrons occurs for lower injected electron flux densities compared to the lowest threshold for a current-driven instability if the electron and ion temperatures are equal. Our results must be used to check for self-consistency of the assumptions used in the interpretation of HXR spectra and of the atmospheric response to the electron injection into the solar plasma.

Figure 2: The ratio of maximum drift speed to electron thermal speed for a range of injected energy flux densities (x-axis) and co- spatial coronal temperatures (y-axis) and for two coronal density values (3 x 10⁹ and 3 1x 10¹⁰ cm^-3, on the left and right panels, respectively. Various curves are also overplotted that show (1) the conditions for the return current to be carried by 1% runaway electrons. This is a somewhat arbitrary number showing the limit between purely collisional and quasi-collisionless propagation. (2) The threshold for a current driven instability to be generated if the electron and ion temperatures are equal. Note that contrary to the runaway acceleration, this threshold is not calculated self-consistently. (3) The threshold for the quasi-collisionless model in our paper to be a valid approximation for energy losses at a normalized RC electric field of 0.15.

Conclusions

Return currents are non-negligible under the conditions defined in this paper. Specifically, for sufficiently large injected flux densities and/or sufficiently low temperatures, the return current is a drifting Maxwellian or a Maxwellian with a runaway tail with significant energy losses. Additional work needs to be done to build self-consistent models of the beam/return-current propagation especially at the highest injected flux densities and/or sufficiently low co-spatial temperatures and densities.

References

[1] "Role of Suprathermal Runaway Electrons Returning to the Acceleration Region in Solar Flares"

[2] "Reduction of the Downward Energy Flux of Nonthermal Electrons in the Solar Flare Corona due to Cospatial Return-current Losses"