On turbulent magnetic reconnection: fast and slow mean steady-states
| Nugget | |
|---|---|
| Number: | 494 |
| 1st Author: | Sage STANISH |
| 2nd Author: | David MacTAGGART |
| Published: | April 28, 2025 |
| Next Nugget: | |
| Previous Nugget: | Quasi-Periodic Pulsations in Ionospheric TEC and Flare EUV |
Introduction
Magnetic reconnection is one of the cornerstones of plasma dynamics in the solar atmosphere (and beyond). It describes the change in connectivity between plasma elements and magnetic field lines and the transference of magnetic flux across topological boundaries of connectivity, actions that are not possible for classical ideal motion. Historically, and still today, the basic framework for understanding magnetic reconnection is to consider it at a two-dimensional null point. This setup has also provided much of the language with which we describe magnetic reconnection. Two characteristic steady-state solutions have been found for this setup, the (slow) Sweet- Parker solution and the (fast) Petschek solution. Debate arises when arguing what the key physics is underlying these solutions.
What about turbulence?
Discussions of Sweet-Parker vs Petschek normally relate to the effects of microphysics, i.e. to the extra terms in a generalized Ohms law that determine how a plasma deviates from ideal magnetohydrodynamics (MHD). With reconnection in astrophysical contexts often occurring in collisionless plasmas, a consideration of the effects of a generalized Ohm's law is very important. However, another factor that may play an equally or even more important role is that of turbulence. The solar corona is a turbulent environment (e.g. Ref. [1]). The corona consists of large-scale magnetic fields that can exist for a long time (i.e. much longer than the turbulent eddy turnover time) and small-scale and short-lived fluctuations. It is these fluctuations that can mediate magnetic reconnection via a turbulent cascade and enhance the effective magnetic resistivity independently of the exact physical dissipation mechanism included in Ohm's law. This is analogous to the effects of turbulent mixing in hydrodynamics.
Turbulent reconnection
Assuming the separation of scale described above, averaging the MHD equations leads to mean and fluctuating equations. In the mean induction equation, the new term is an electromotive force, which can be argued to dominate non-ideal collisionless and resistive terms over the inertial range (e.g. Ref. [2]) It is the electromotive force, due to turbulence, that can drive reconnection.
Steady states
To model the electromotive force, we turn to a turbulent reconnection model (Ref. [3]). Here, the electromotive force is determined by one-point statistical properties of turbulence which have their own evolution equations. In particular, the main properties are the turbulent energy and the cross-helicity.
By considering the turbulent timescale as a parameter, it is possible to generate both Sweet-Parker and Petschek solutions that are approximately steady (for the mean field). Examples of the profiles of these solutions are shown below.
The Sweet-Parker solution arises when the turbulent timescale is too short to allow the turbulent energy to grow and have any effect on the mean field. The Sweet-Parker solution can, therefore, be considered a laminar (non-turbulent) solution. The Petschek solution arises when the turbulent energy is able to grow and concentrate at the null point. All the Petschek solutions converge to the same (fast) reconnection rate.
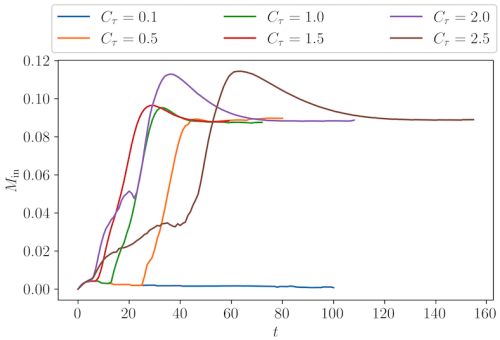
Conclusions
Turbulence is a natural means for producing fast reconnection. When simulating magnetic fields on scales such as those of active regions, for which it is not possible to resolve individual turbulent fluctuations, an approach such as that described above is capable of producing the fast reconnection needed for solar atmosphere phenomena.
Further details can be found in Ref. [4].
References
[1] "Metis Observation of the Onset of Fully Developed Turbulence in the Solar Corona"
[2] "Turbulent General Magnetic Reconnection"
[3] "Explosive Turbulent Magnetic Reconnection"
[4] "On turbulent magnetic reconnection: fast and slow mean steady-states"
