Return-current Model Spectra and Enhanced Plasma Resistivity

Nugget
Number:	259
1st Author:	Meriem Alaoui
2nd Author:	and Gordon Holman
Published:	31 August 2015
Next Nugget:
Previous Nugget:	Cosmic rays and the coronal B field

Introduction

Solar flares involve sudden brightening across the whole range of the electromagnetic spectrum, and in particular the hard X-ray emission has proved to be a crucial factor in deciphering flare physics. The most common hard X-ray emission is an "impulsive" source that seems to define the main energy release of a flare, although other more gradual energy releases may also take place. The hard X-rays come from bremsstrahlung, a very inefficient emission mechanism, and the mere existence of hard X-ray sources implies a large amount of energy in energetic electrons.

The "number problem"

In the late 1970's several authors estimated the number of electrons in the downward-streaming beam thought to be required to explain the observed X-ray bremsstrahlung emission, and concluded that it must be several orders of magnitude higher than the number of electrons in the active region corona, where the acceleration would take place. This has been referred to as the electron number problem in solar flares: (1) Where do all the electrons come from that produce the bremsstrahlung emission, which may last from a few seconds to a few minutes? (2) What keeps the electron beam stable to charge separation and magnetic pinching? A co-spatial return current has been proposed to answer these questions. This current would flow in the opposite direction to the direct current created by the downward-streaming electrons. We consider it here as co-spatial and steady-state, serving to resupply the acceleration region with electrons from the thermal background and also to ensure that the beam is stable. The return current affects the shape of the X-ray spectrum by creating a flattening at lower energies due to a potential drop from the acceleration region to the thick target (Ref. [1]), where electrons are collisionally stopped and generate bremsstrahlung. In the following, we tested whether a return-current model can provide acceptable fits to the RHESSI spectra. Note that an earlier Nugget deals with related aspects of these problems.

We have found (Ref. [2]) that spectra with strong breaks can be fitted with a return current model. We fitted 206 spatially integrated spectra from 16 RHESSI flares with a co-spatial return-current model to deduce the potential drop that drives the return current and causes the spectral flattening. This fixes the injected spectral index, the electron flux at 50 keV, the low-energy cutoff and any high-energy cutoff at injection. We then deduce plasma parameters such as the resistivity. This resistivity was found to be up to eight orders of magnitude greater than the classical resistivity deduced from temperatures obtained from the RHESSI spectral fits!

Return current collisional thick-target model: the RCCTTM

The assumptions of the model are as follows:

Injected single power-law electron flux density distribution with a sharp low-energy cutoff E_c and a high-energy cutoff E_high.

Steady-state electric-field-driven return current with electrons streaming along the loop, balanced by a co-spatial return current in the opposite direction, for which j_RC = j_direct.

Return-current losses are considered throughout the loop until electrons reach the target, where they lose all their remaining energy by Coulomb collisions.

The observed hard X-ray spectral flattening at lower energies is due to the return current. This is achieved by choosing flare spectra with strong enough breaks that cannot be explained with non-uniform target ionization and X-ray Compton albedo alone. We first fit the spectra with a spectral model having an insignicant low-energy cutoff (at 2 keV) to insure that the contribution to the spectral flattening at lower energies is due solely to the potential drop. We then fix the potential drop and fit the spectra with the highest low-energy cutoff that keeps the Χ² within one sigma of the best-fit value.

Figure 1: Return-current collisional thick-target model cartoon. Electrons are accelerated near the top of the loop, and lose their energy due to the potential drop along the loop before they reach the chromosphere, where the density is high enough for Coulomb collisions to dominate.

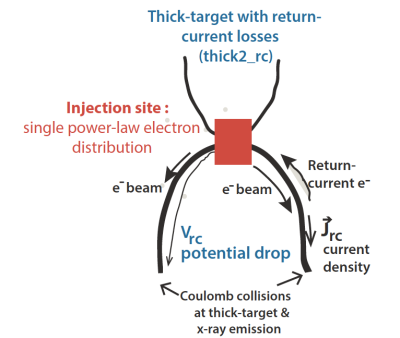
3. Fitted parameters and resistivity in the plasma

We find that the RCCTTM provides good fits to RHESSI spectra with strong breaks or flattenings at lower energies. Figure 2 shows fit parameters from the flare SOL2002-06-02. The fit parameters of our return current model (currently in RHESSI's OSPEX software under "thick2 rc") are the return-current potential drop, the spectral index from the acceleration region, the electron flux at 50 keV, and the low-energy cutoff. This was a rare case for which a high-energy cutoff significantly improved the spectral fits in four time intervals.

Figure 2: Example of fitted and derived parameters with return-current model for the flare SOL2002-06-02. Left axis: fitted potential drop (red) and 68% condence level from Monte Carlo runs (pink), energy flux density using the upper limit to the low-energy cutoff (dark blue), hard X-ray flux at 50 keV (green). Right axis: spectral index at acceleration region(light blue). It is interesting to note that this are shows a soft-hard-soft behavior at the acceleration region (anti-correlation of spectral index and HXR fluxes), and soft-hard-soft behavior at the footpoints (correlation between HXR flux and potential drop).

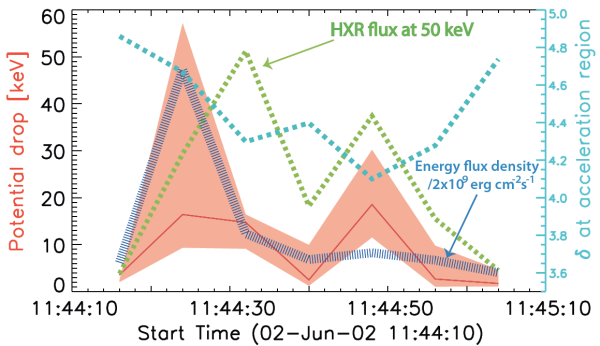
An interesting parameter is the resistivity, which we deduce from the potential drop and the electron flux density using Ohm's law, with the electric field given by the potential drop and the loop half-length, and the current density given by the electron flux density (we estimate the source sizes from RHESSI images of the loop and footpoint area). We proceeded then to compare this inferred resistivity with the theoretical Spitzer resistivity at the temperature derived from the RHESSI spectral fits and at a much lower, chromospheric, temperature. The Spitzer resistivity is due to electron-ion collisions and is proportional to T^-3/2.

Figure 3: Resistivity vs. temperature scatter plot. The green and orange lines represent the Spitzer resistivity at the fitted temperature, which is around 20 MK, and at 10⁴ K, respectively.

Conclusions

In Ref. [2] we describe this project in more detail, and draw the following basic conclusions.

The return-current collisional thick-target model (RCCTTM) provides acceptable fits to RHESSI data with strong spectral breaks. The flattening of the X-ray spectrum is explained by a potential drop from the acceleration region to the thick-target.

Using the fitted parameters, we can derive the resistivity in the plasma that electrons encounter along their path to the thick target. We find that these resistivities are typically enhanced by one to eight orders of magnitude compared to the Spitzer values at T around 20 MK. In cases where the resistivity is higher than the Spitzer value at T = 10⁴ K, which could feasibly be present along the legs of the flare loops, we can confidently conclude that the resistivity is high enough to require the presence of turbulence (anomalous resistivity).

References

[1] "Understanding the Impact of Return-current Losses on the X-Ray Emission from Solar Flares"

[2] Alaoui & Holman (article in preparation) "Understanding X-ray spectra: Evaluation of a co-spatial return-current model."